Transformada de Laplace (Transformada de una derivada) (Parte 2)
Categories: Transforma de Laplace
Inicio
> Transforma de Laplace > Transformada de Laplace (Transformada de una derivada) (Parte 2)
Curso de Integrales Multiples
Profesor, despues de ver los videos y leer hasta el final sobre el tema, se me ocurre una idea que no se si sea válida,
la idea es:
que tal si cuando llego a Y(s) = 1/[(S-2)(S-3)] + 1/(S-3) (Minuto 6:30)
aplico convolución a 1/[(S-2)(S-3)] directamente y
transf inversa al 1/(S-3) directamente también,
es posible?
si podes hacer convolucion en
para que te quede 
y el otro por inversa queda de una vez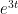 
y sumas, y listo.
Por que el cambio de signo para el 1/(S-3) en el minuto 4:40 ?? No entiendo! segun mis calculos deberia ser :
Y(s) = 1/[(S-2)(S-3)] + 1/(S-3) y no 1/[(S-2)(S-3)] – 1/(S-3)
Corrijanme si estoy en un error por favor
Si es un error en ese signo deberia de ser